Acoustic Metamaterials & Waves in Periodic Structures
This page displays the different studies that I have been working on under the topic of acoustic metamaterials:
Slow Sound Metamaterials & Perfect Absorption

Acoustic metamaterials are characterized by their locally resonant unit cells. A basic example of an acoustic metamaterial could consist of a duct loaded by a series of Helmholtz resonators. These act as resonant scatterers into the tube, introducing a strong dispersion relation in the system. This means that the propagation speed of the sound waves travelling in the section of the duct ruled by the resonators changes in function of the frequency, where the the wavenumber k would increase significantly until a band-gap is created, i.e., a range of frequencies where the real part of the wavenumber becomes null and its imaginary part increases, with a peak at the resonant frequency of the locally resonant element. This implies an absence of propagating waves aroud such frequencies despite the system being open on both sides. The more resonators in such a system, the broader the band-gap where waves cannot propagate.
Yet, before reaching this band-gap, a very interesting phenomenon can be observed. Due to the linear relation between the wavenumber and the propagation speed of the wave in the medium, when the real part of the wavenumber k increases before the band-gap, the propagation speed of the wave c would inversely decrease, up the the point where it would reach zero while in the band-gap regime. By reducing the propagating speed of sound, a parameter in the relation of the resonant frequency of the Helmholtz resonator, this also reduces the frequency at which the resonator would react. This allows to design acoustic metamaterials that effectively work for wavelengths much larger than what any traditional acoustic treatment would allow. The system is then said to work on a deep-subwavelength regime

Slow sound can be used for designing deep-subwavelength treatments for acoustic absorption or sound diffusion, allowing the design of ultra-thin structures with optimal acoustic properties, with dimensions orders of magntidude thinner than their traditional counterparts.
Losses are an important part of the design strategy of acoustic metamaterials. More specifically, the losses induced by the acoustic boundary layers can be exploited in order to create perfect absorbers. Here, an open lossy resonator loaded in a very thin slit is critically coupled with the outside duct, resulting in a (quasi)total absorption of sound. It can be noted that even with one resonator in the slit, the propagating sound wave inside the slit is drastically slowed when entering the slit, due to the visco-thermal losses induced by the acoustic boundary layer.
Metamateriaux pour l'acoustique audible: Absorption parfaite et diffusion sublongueur d'onde,
V. Romero-García, V. Pagneux, J.-P. Groby, N. Jiménez, E. Ballestero,
Acoustique & Techniques, 94/95:33-39, 2020.
Metadiffusers : Ultra-Thin Sound Diffusers

In this research topic, innovative acoustic structures for sound diffusion have been developped, called metadiffusers. Sound diffusion refers to the spreading of sound when in contact with an interface. Diffuse reflection of sound is opposed to specular reflection, where the sound waves are reflected as billiard balls would on a pool table. Usually, sound diffusion is achieved through structures called acoustic diffusers, or Schroeder diffusers in honor of the pionneering works or M.R. Schroeder. Metadiffusers are ultra-thin alternatives for sound diffusion treatments, with dimensions orders of magnitude thinner than traditional strategies (10 to 20 times thinner). Metadiffusers not only exhibit high sound diffusion features but also show a stronger potential for geometrical structure optimization.
Metadiffusers for quasi-perfect and broadband sound diffusion,E. Ballestero, N. Jiménez, J.-P. Groby, H. Aygün, S. Dance, V. Romero-García,
Appl. Phys. Lett., 119, 044101, 2021. Metamateriaux pour l'acoustique audible: Absorption parfaite et diffusion sublongueur d'onde,
V. Romero-García, V. Pagneux, J.-P. Groby, N. Jiménez, E. Ballestero,
Acoustique & Techniques, 94/95:33-39, 2020.
Experimental validation of deep-subwavelength diffusion by acoustic metadiffusers,
E. Ballestero, N. Jiménez, J.-P. Groby, H. Aygün, S. Dance, V. Romero-García,
Appl. Phys. Lett., 115, 081901, 2019.

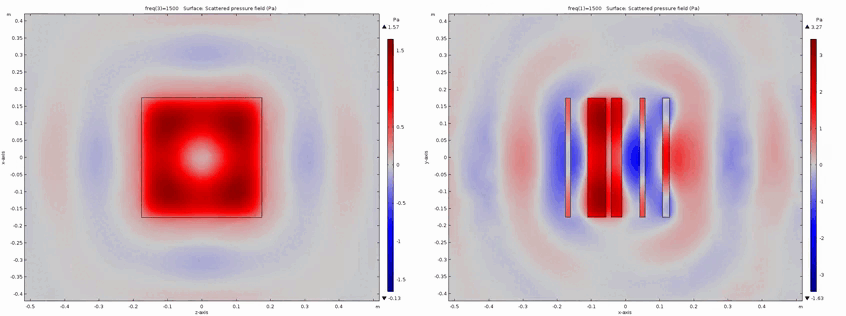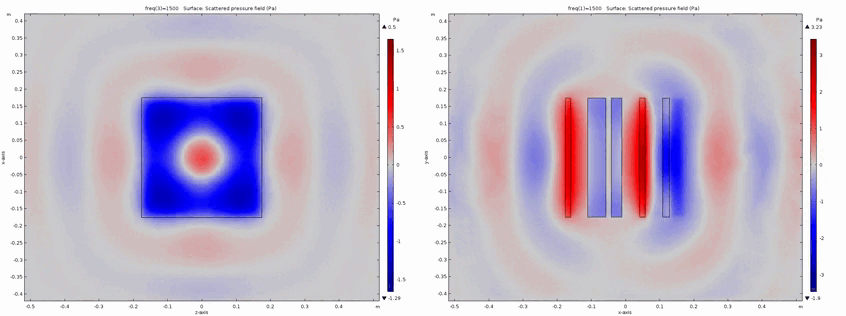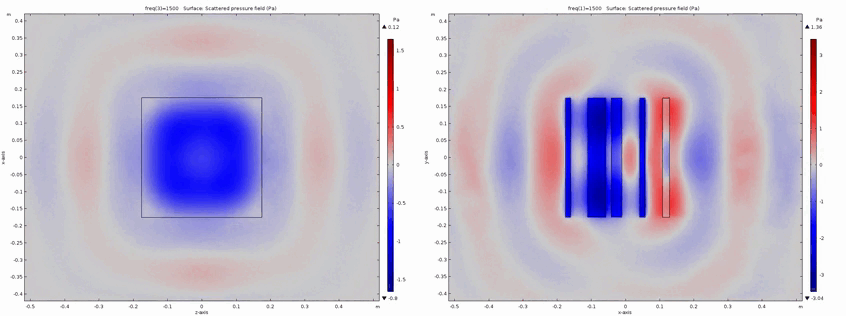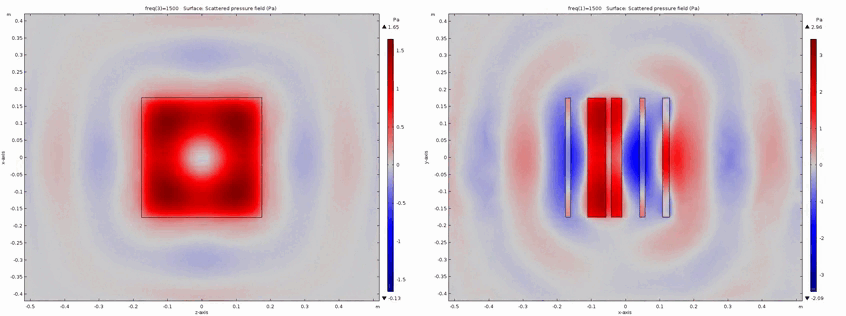
(Top left) Magnitude of the reflection coefficient along the surface of the diffuser. Being 2D diffusers the latter only varies along the x-axis. (Top right) Phase angle of the reflection coefficient along the surface of the diffuser. (Bottom right) Polar far-field scattered pressure from the diffuser. This is dependent of the magnitude and phase of the reflection coefficient. (Bottom left) Normalized sound diffusion coefficient of the diffuser expressed as a spatial autocorrelation function of the scattered pressure distribution, i.e., 1 means perfect diffusion or omni-directional diffusion and 0 means the diffusion reference of a radiating flat surface.
N.B: For each frequency corresponds a magnitude and phase of the reflection coefficient, and thus a polar distribution of the reflected waves, ultimately summing into one number, the diffusion coefficient.